
El teorema más popular en matemática es probablemente el llamado Teorema de Pitágoras, aunque Pitágoras nació en el Siglo VI a.C. no existe evidencia de que por aquellos años Pitágoras o alguien de su escuela descubriera esta propiedad de los triángulos rectángulos. Algunos medios han afirmado que este teorema existía desde 2000 a.C. en las tablillas babilónicas. En este artículo desmentiremos esta versión.
Un teorema matemático es un enunciado atemporal y válido universalmente; para que este enunciado posea validez matemática es necesario que cuente con una “demostración rigurosa”. Para obtener una demostración rigurosa de un enunciado matemático es necesario establecer un “sistema formal” que lo sostenga. El primer sistema formal inventado por los seres humanos fue el “sistema axiomático griego” que se remonta al año 300 a.C. En aquella época, el sistema formal estaba conformado por definiciones, postulados (axiomas) y gobernado por leyes del pensamiento aristotélico (principio de identidad, principio de no contradicción, principio del tercio excluido). Con este sistema se inicia el proceso hipotético deductivo que caracteriza al pensamiento matemático hasta nuestros días. Con esta base rigurosa se empezó a construir un cuerpo de conocimiento que hoy llamamos matemática.
¿De dónde salió que el Teorema de Pitágoras se encuentra en las tablillas babilónicas? Salió del desconocimiento histórico y matemático. Si bien es cierto que en la tablilla Plimpton 322, se encontraron seis columnas de números incompletas en donde la primera columna es la numeración del 1 al 15, si los cuadrados de los números de la columna II se restan con los cuadrados de la columna III, se obtiene un cuadrado ( c2 – b2 = a2 ) que se encuentra en una quinta columna incompleta. Estos datos de 15 triángulos rectángulos no constituyen un teorema matemático y es muy probable que fueran obtenidas empíricamente, ante la necesidad de tener cálculos para ser usados en problemas de medición de tierras, en construcciones o repartición de herencias.
Muchas veces se comete el error de asociar estas evidencias empíricas con algo ya conocido, en este caso con el Teorema de Pitágoras. Una verificación empírica no representa una demostración matemática.
La tabilla Plimpton 322 no constituye una prueba fehaciente de que los antiguos babilonios hubieran creado un sistema axiomático capaz de probar que cualquier triángulo rectángulo plano cumple “la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa”. Simplemente porque en 2000 a.C. la matemática tenía naturaleza empírica, sólo resolvía problemas particulares, no existían “leyes matemáticas universales” como para poder afirmar que el Teorema de Pitágoras existía en la época babilónica.
Como teorema no existía (y ningún teorema) en la época babilónica puesto que no había las herramientas matemáticas para demostrar este enunciado, sólo se realizaban mediciones empíricas útiles para la vida cotidiana. En una sexta columna de la tablilla de Plimpton se establecía el cociente entre la hipotenusa y los catetos del triángulo rectángulo, muchos interpretan que los antiguos babilonios conocían las “razones trigonométricas”, no existe evidencia de que se conociera como “concepto”; y muchos menos existe evidencia de una definición. Los griegos (Hiparco de Nicea) fueron los primeros en establecer las razones trigonométricas con definiciones precisas para usos astronómicos.
Estos errores son comunes en las redes sociales y páginas web (hasta en Wikipedia) muchas veces se toman como ciertas. En el caso del Teorema de Pitágoras también se afirmó que era un hallazgo reciente. La tabilla Plimpton 322 fue descubierta por George Plimpton en 1922 en una compra fortuita; si algún investigador de la historia de la matemática afirmó que los babilonios conocían el Teorema de Pitágoras, cometió el error de asociarlo con el teorema conocido hoy día.
No se sabe si fue Pitágoras o alguien de su escuela el primero que lo demostró; lo cierto es que aparece demostrado por primera vez en la historia de la matemática en la Proposición 47 de libro I de los Elementos, de Euclides (300 a.C.); fue en esta obra en donde se oficializó el primer sistema formal axiomático y en ese momento nacieron oficialmente los primeros teoremas matemáticos tal como los conocemos, entre ellos el Teorema de Pitágoras.
Notas relacionadas
- ¿Por qué no se puede dividir por cero?
- 18 enero, 2025
Toda afirmación en matemática es siempre referida a un determinado sistema formal.
- Fourier y su contribución a la matemática moderna
- 27 abril, 2024
Fourier consideraba que toda función continua puede representarse como una serie infinita de senos y cosenos.
- El cerebro matemático
- 14 junio, 2025
Este cerebro racional, con millones de conexiones neuronales, es también emocional, e ilógico.
- Sobre la tecnología en la enseñanza de la matemática
- 31 mayo, 2025
La incursión de las herramientas tecnológicas en la enseñanza de la matemática lleva varias décadas.

- Luca Pacioli: el primer retrato de un matemático
- 16 marzo, 2025
Luca Pacioli fue matemático, contador y profesor universitario.

- Sophus Lie y su teoría de transformaciones continuas
- 28 abril, 2025
Matemático universal, capaz de conectar las ecuaciones diferenciales y el álgebra abstracta.

- La historia del Premio Abel
- 08 marzo, 2025
Es sabido que no existe un premio Nobel para matemáticos.

- Sobre el libro Geometría Plana y del espacio de Aurelio Baldor
- 08 febrero, 2025
El primer libro escrito por el profesor Baldor, fue su Álgebra, publicada en 1941, adoptado como texto oficial en Cuba.

- Emmy Noether: la señora de los anillos
- 10 mayo, 2025
Alguna vez Albert Einstein dijo: según el juicio de los más eminentes matemáticos en vida, Emmy Noether era la más importante inteligencia matemática creativa que ha nacido desde que comenzó la educación superior de las mujeres.

- La invención del infinito actual
- 19 octubre, 2024
Los objetos matemáticos, como constructos, se conciben en la mente humana; para ello se debe tener una idea precisa para formalizarlos y que luego emerjan sus propiedades.

- Matemáticas, Borges y Los crímenes de Oxford
- 01 marzo, 2025
En la novela Los crímenes de Oxford, su autor, el doctor en Matemáticas y escritor argentino Guillermo Martínez, es un ejemplo de convergencia de estas dos áreas aparentemente disímiles: matemáticas y literatura.

Los matemáticos no sólo eran conocedores de la génesis de su disciplina, sino que ejercían una alta valoración de la Historia de la Matemática.
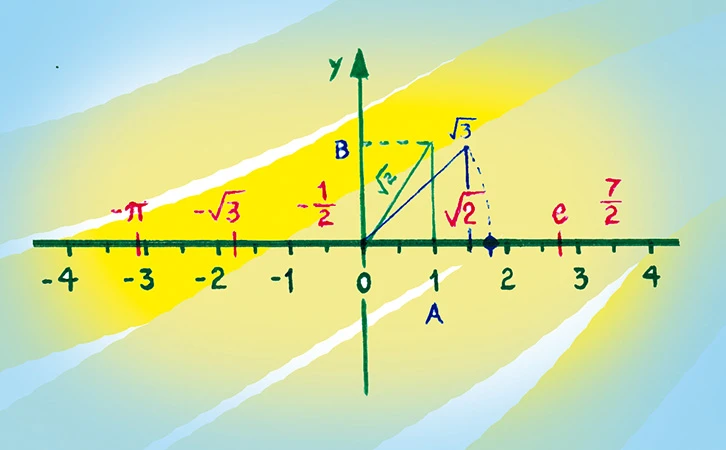
- La recta geométrica y los números reales
- 05 octubre, 2024
La recta geométrica como objeto matemático tiene una naturaleza distinta a los números.

- El hacer matemático en el Siglo XX
- 26 octubre, 2024
Los modos del pensamiento matemático influyen en su hacer, el Siglo XX ha sido testigo de al menos dos formas de este hacer, con marcada influencia ideológica.

- Dios creó a los números, de Stephen Hawking
- 22 marzo, 2025
Dios creó a los números es el titulo de una de las obras más importantes del gran científico y divulgador Stephen Hawking.
Opinión
Editorial
El Gas Bienestar también resultó demagogia
Se fue AMLO y su objetivo principal quedó muy lejos de alcanzarse.
Las más leídas
Dan sentencia definitiva a Cuauhtémoc Blanco por violencia política de género
Casi un millón de estudiantes abandonaron la escuela en el ciclo 2024-2025
Trabajadores de Pemex lanzan campaña por una jubilación digna
Van contra la opacidad en la medición de la pobreza; distintas ONG lanzan iniciativa propia
En fase piloto la reforma laboral para trabajadores de plataformas digitales
El PACIC, otro fracaso que la 4T no admite











Escrito por Dr. Esptiben Rojas Bernilla
Colaborador