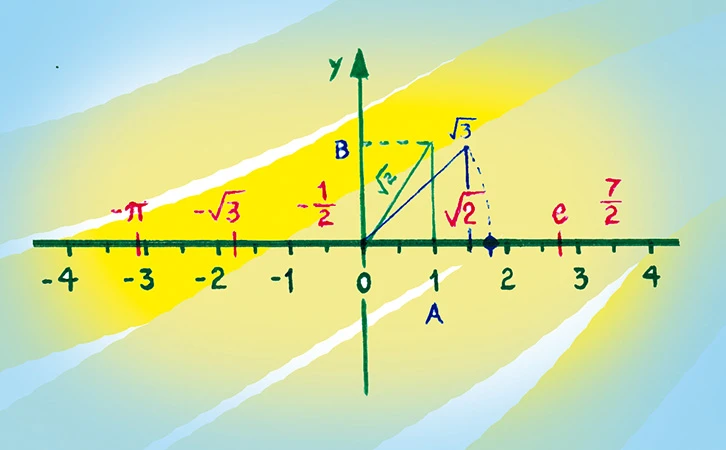
Gran parte del trabajo matemático radica en establecer conexiones o puentes entre objetos matemáticos de naturaleza distinta. Por ejemplo, la recta geométrica como objeto matemático tiene una naturaleza distinta a los números; generar una isovalencia entre ellos tardó 25 siglos de desarrollo matemático. En todo este periodo, no toda parte de una recta geométrica era susceptible de asociarle una magnitud (medida), por ejemplo, no se podía medir con exactitud la hipotenusa de un triángulo rectángulo cuyos catetos miden una unidad. Sólo era posible establecer una aproximación, y no el número concreto asociado a esta hipotenusa. Estas cosas generaron el siguiente problema: Si pretendemos asociar o identificar los puntos de la recta geométrica con los números (hasta la primera mitad del Siglo XIX, sólo se consideraban números a los enteros y a los racionales), es suficiente fijar un punto en la recta geométrica y una unidad de medida para llevar a cabo la asociación deseada. Primeramente, al punto fijo se le asocia el número cero, y con la unidad establecida se asocia a la derecha del cero el 1, luego el 2 y así sucesivamente, y a la izquierda del cero con la misma unidad de medida se va asociando el -1, luego el -2, y así sucesivamente. Incluso las fracciones tienen un lugar en la recta geométrica. Todo este trabajo es muy relativo al punto fijo elegido y a la unidad establecida, no existe una asociación absoluta de tales objetos (puntos y números), desde ahí existe un problema de inexactitud y constituye un ejemplo para demostrar que la matemática no es algo exacto como se cree, sino siempre relativa a un contexto matemático; para pretender una exactitud tenemos que formalizar cada acto como una invención humana.
Podemos preguntarnos ¿qué punto le corresponde a la longitud de la hipotenusa de un triángulo rectángulo de catetos que miden la unidad? Es decir, será posible ubicar lo que hoy llamamos en una recta geométrica de manera exacta, ¿quién puede hacerlo? Dudo que exista un ser humano que pueda ubicar el punto exacto que le corresponde. Se establece una ruptura cognitiva, que hasta el día de hoy persiste, debido a las limitaciones de la mente humana. Este problema fue resuelto desde el punto de vista matemático por Richard Dedekind en 1878, desde este momento fue posible conectar biyectivamente los puntos de la recta geométrica y los números que por primera vez incluían a los irracionales , , es decir, estos hoyos que poseía la recta geométrica fueron cubiertos por estos nuevos objetos numéricos, técnicamente se le llama completación de la recta real. Pasó a ser la recta geométrica un objeto continuo, identificable cada uno de sus puntos con un número real, dando un fundamento riguroso al concepto de límite o punto de acumulación en la recta y así fundamentar el naciente análisis matemático.
Hoy en día se ha establecido en el discurso matemático escolar esta asociación entre los puntos de la recta geométrica y los números reales, apelando a la intuición de los estudiantes se ubica a estos números irracionales en la recta geométrica. Por supuesto que la intuición no es ninguna garantía de certeza, humanamente seguimos sin ubicar exactamente el punto que corresponde a los números irracionales. Aquí existe algo inalcanzable para la mente humana.
La forma en que matemáticamente hemos dado existencia a los números irracionales ha sido con base en la idea de convergencia o aproximación, es decir, la formalización de una idea muy antigua, debido al griego Eudoxio y luego refinada por Agustín Cauchy y Karl Weierstrass, hemos tratado de capturar conceptualmente lo arbitrariamente pequeño mediante una definición formal. De esa manera, Richard Dedekind, con sus famosas cortaduras, y luego George Cantor, con su convergencia de sucesiones de Cauchy de racionales, dieron existencia a objetos matemáticos que existen en lo formal, pero que su naturaleza ontológica aún queda en el limbo de la mente humana.
En este sentido, la concepción ficcionalista de los objetos matemáticos, en particular de los números irracionales, recobra sentido, esclarece su naturaleza y nos permite ver a la matemática como un gran constructo cuya existencia sólo se encuentra en la mente humana.
Notas relacionadas
- El cerebro matemático
- 14 junio, 2025
Este cerebro racional, con millones de conexiones neuronales, es también emocional, e ilógico.

- El club de los matemáticos
- 15 febrero, 2025
El club de los matemáticos está constituido por un conjunto de seres humanos con alta formación matemática y capaces de inventar nuevos teoremas.

- La historia del premio Abel
- 06 julio, 2024
El Premio Abel puede considerarse como el premio Nobel para matemáticos.

- Los romances de Albert Einstein en la Guerra Fría
- 12 abril, 2025
No vamos a juzgar la vida privada de este gran científico, la reflexión es aprender a separar los logros científicos de una persona y sus debilidades humanas.

- La psicología de Gottfried Leibniz
- 13 mayo, 2024
La personalidad de Gottfried Leibniz, lo convertía en un brillante diplomático.

- Entre la Historia y la Matemática
- 30 marzo, 2024
El tránsito hacia una matemática filosófica exige iniciar una quinta revolución matemática; para ello, el estudio de la historia desde el hacer de un matemático es fundamental.

- La psicología de Isaac Newton
- 08 mayo, 2024
La tenacidad en su trabajo le acompañó hasta una edad muy avanzada.

- Infinitos de distinto tamaño
- 09 noviembre, 2024
Uno de los conceptos que más ha apasionado a los seres humanos es la idea de infinito.
- Fourier y su contribución a la matemática moderna
- 27 abril, 2024
Fourier consideraba que toda función continua puede representarse como una serie infinita de senos y cosenos.

- ¿Por qué el 1 no es un número primo?
- 21 septiembre, 2024
A Pitágoras se le atribuye la idea conceptual de “primo”.

- Entre la matemática y la transposición didáctica
- 28 septiembre, 2024
En la primera mitad del Siglo XX aparece el fenómeno de la masificación de la educación matemática, periodo en que la matemática entra en la revolución del formalismo hilbertiano.

- Luca Pacioli: el primer retrato de un matemático
- 16 marzo, 2025
Luca Pacioli fue matemático, contador y profesor universitario.

- Escribir libros de matemática o papers
- 14 septiembre, 2024
Ninguno de estos libros me parece copia o similares a los libros estándar.
- La protomatemática
- 24 mayo, 2025
A principios del Siglo XX se descubrieron tablillas de arcilla en Irak y papiros en Egipto que contenían problemas y soluciones con data de cinco mil a cuatro mil años.

- Matemática y su aprendizaje
- 23 noviembre, 2024
El cerebro no aprende matemática si no se enfrenta a algo difícil, o por lo menos desafiante, que rete su imaginación y saque todo su potencial.
Opinión
Editorial
Los datos personales y el “espionaje de Estado”
El segundo tema se refiere a la veloz aprobación de 16 leyes realizada a principios del presente mes en el Congreso de la Unión.
Las más leídas
¡Sí o sí! CURP Biométrica será obligatoria a partir de 2026, pese a riesgo de hackers
Intensifican el 'maiceo', ahora Gobierno dará dinero por bebés
Alerta, ganaderos de Durango temen ingreso de reses con gusano barrenador
Jitomateros de San Quintín, los más afectados por impuesto de Trump
Pese a adeudos con el SAT, gobierno de la CDMX da contrato millonario a Salinas Pliego
Pese a abstencionismo y protestas, Patricia Zarza es rectora electa de UAEMéx











Escrito por Dr. Esptiben Rojas Bernilla
Colaborador