
La ruleta es el ícono de los juegos de azar. Este sencillo y misterioso juego, en un tiempo prohibido, tildado de “truculento” y hasta “diabólico”, despierta en las personas las más intensas pasiones. En segundos puede volver rico al mendigo y terriblemente desgraciado al millonario.
Lo maligno del juego no estriba, por ejemplo, en que sus números sumen 666 (37X36/2, según la fórmula de Gauss) sino en los efectos que produce en quien es dominado por él.
En La piel de zapa, Honoré de Balzac (1799-1850) nos muestra cómo un hombre bueno y brillante es capaz de vender la cripta con los restos de su madre para salir de sus deudas y seguir jugando, y de cambiar su propia vida por un amuleto que cumpla sus deseos.
En Veinticuatro horas en la vida de una mujer, de Stefan Zweig (1881-1942), el protagonista, trastornado por el juego, humilla públicamente a la mujer que le salvó del suicidio. Arroja limosnas a quien le quitó el hambre e insultos a quien le dio su amor.
¿Y qué ocurre en el terreno de la ciencia? En su libro Cuando los físicos asaltaron los mercados, James Weatherall documenta la historia real de tres eminentes científicos que unieron fuerzas para vencer a la ruleta. Se trata de Edward Thorp (profesor de física y matemáticas del MIT), Claude Shannon (ingeniero eléctrico del MIT y fundador de la teoría de la información) y John Kelly (físico experto en telecomunicaciones). La ruleta es un mecanismo aleatorio (cada tirada es independiente de la anterior), por tanto, trataron de ganar aplicando las leyes de la física, en particular, del movimiento circular. Conociendo la velocidad de la ruleta y la posición inicial de la bola es posible determinar en qué región es más probable que ésta se detenga. La operación se llevó a cabo en Las Vegas en 1961, conjuntando la teoría del juego de Thorp, los dispositivos electrónicos diseñados por Shannon y la teoría de la información aplicada a las apuestas de Kelly. La prueba falló porque el auricular de Thorp fue descubierto.
La ruleta fue inventada por el físico matemático francés Blaise Pascal en el Siglo XVII. La versión europea tiene 18 números rojos, 18 negros y el cero. La versión americana tiene, además, un doble cero. ¿Cómo es que las probabilidades y las reglas del pago favorecen a la casa?
Si se apuesta a un solo número la probabilidad de ganar es de 1/37 y la de perder de 36/37, pero el premio se paga 35 a 1. De este modo, se espera que, en promedio, si se juegan 37 veces apostando un dólar se gane una vez y se pierdan 36, pero el pago será de solo 35 dólares. El beneficio esperado es siempre menor que la pérdida esperada y, por tanto, la utilidad es negativa. Aplicando un análisis probabilístico para diferente número de tiradas y distintos tipos de apuestas se obtienen resultados similares (desfavorables para el jugador). Esto ocurre apostando a rojos, a negros, a pares, a impares, docenas, tercias, parejas, etc. Tanto si se juega una o varias veces como si se aplican distintas estrategias de apuestas, (como la “martingala”, que consiste en ir duplicando el monto apostado) la probabilidad y las reglas de pago van en contra del jugador.
En la ruleta los resultados son equiprobables, no hay predilección por ningún número o color. Por la Ley de los grandes números, a la larga todos los valores tenderán a aparecer con la misma frecuencia.
Pésimo negocio, pues, “jugar en Roulletenburg”. En esta ciudad ficticia se desarrolla la novela El jugador de Fíodor Dostoievski (1821–1881), quien también era ludópata. Su obra muestra la hipocresía de la aristocracia y la ingenuidad de los pobres que creen que apostando una moneda cambiarán su condición. “Si me posees, lo poseerás todo, pero tu vida me pertenecerá”, dicen a un tiempo el maléfico amuleto de Balzac, la ruleta y los intereses económicos detrás del croupier.
Notas relacionadas

- Cuando las cuentas fallan
- 28 marzo, 2021
Las matemáticas dieron orden al caos. Dan certeza en el momento que se vive y ayudan a comprender y medir los fenómenos que rodean a las personas.

- La riqueza genética del ser humano
- 19 marzo, 2022
Nuestras características físicas son resultado de la combinación de nuestros genes y entorno. Cada quien es distinto: tiene una combinación única de genes y ha sido moldeada por la realidad en que se desarrolla antes y después de nacer.
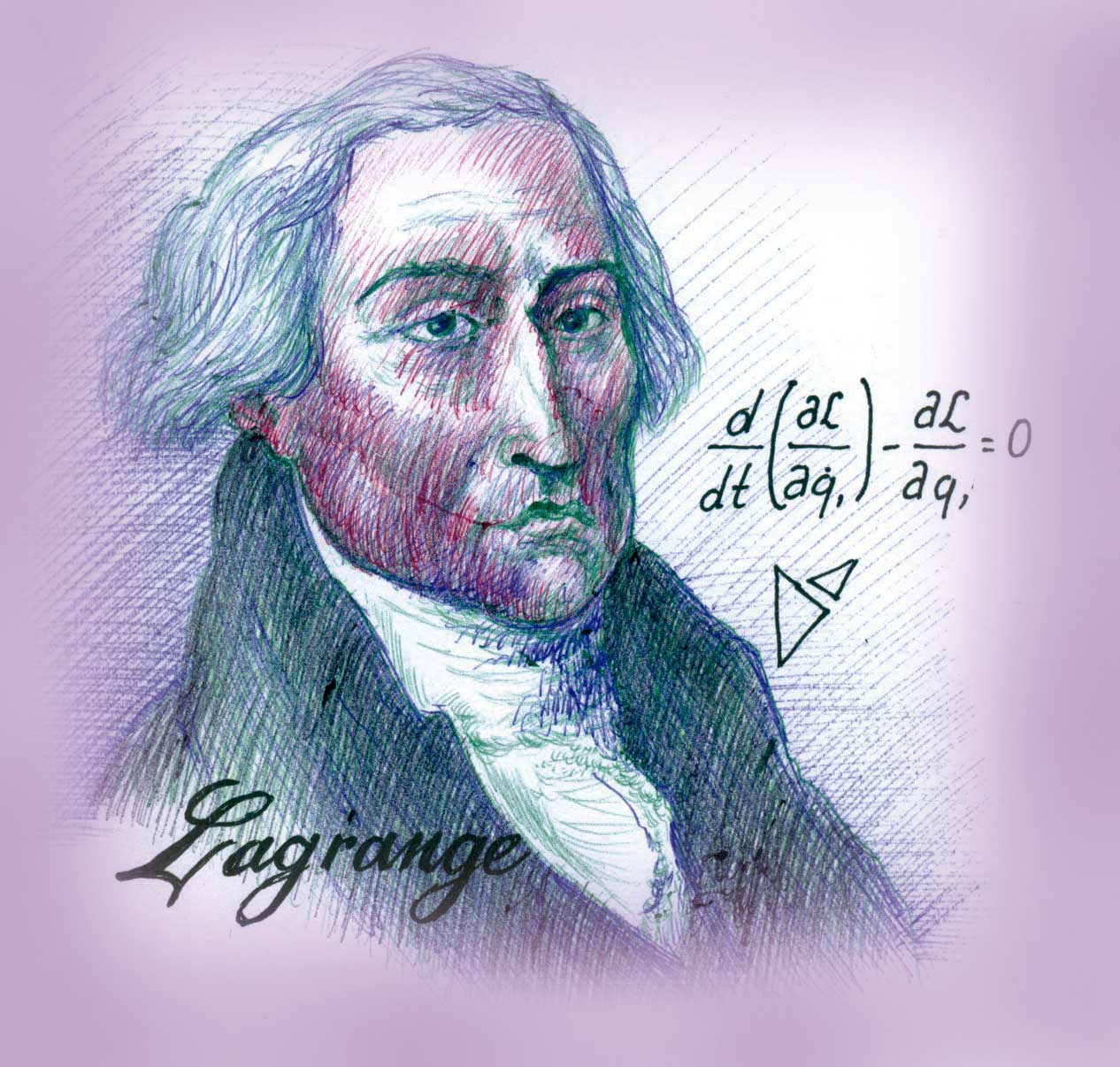
- Joseph Louis Lagrange: el gran analista de la ilustración
- 13 junio, 2021
Considerado de los grandes matemáticos del S. XVIII, su mente no era la de un geómetra, era esencialmente analista. Newton, Euler y D’ Alembert, reconocieron que sus métodos analíticos los habían ayudado a entender problemas matemáticos.

- Reaparece tiburón de más de 500 años
- 15 noviembre, 2023
El comportamiento migratorio de los tiburones de Groenlandia aún es un misterio para la comunidad científica.

- Napoleón Bonaparte y los matemáticos
- 14 abril, 2024
Durante el gobierno de Napoleón, Francia vivió una época brillante para la ciencia, se hablaba del Imperio de las Ciencias.

- Función del sistema respiratorio durante el ejercicio físico
- 02 marzo, 2024
En este artículo sarás por qué es tan importante saber respirar bien cuando realizas algún tipo de ejercicio físico.

- El Gran Cerro Humeante
- 29 mayo, 2023
El volcán Popocatépetl se formó hace 23 mil años sobre los restos de otros volcanes. Desde entonces presenta actividad de manera intermitente, Tras estar inactivo 67 años, "despertó" en 1994.

Mirar directamente al Sol durante un eclipse puede causar daños irreversibles en la retina, incluso sin sentir dolor; como sucedió en 1991.

- Tres físicos y tres escritores contra el croupier
- 08 junio, 2024
En la ruleta los resultados son equiprobables, no hay predilección por ningún número o color.

- Avanzan estudios para prótesis visuales
- 07 agosto, 2019
La intención es lograr un lente de material blando que logre un acercamiento, en un primer prototipo, de 32 por ciento con respecto a la visualización normal.

“Estamos ante la presencia del gobierno que intenta ver como accidentes, lo que más bien han sido tragedias provocadas por la ausencia de mantenimiento”, denunció Andrés Atayde, presidente del PAN.

- ¿Por qué aumentan los resfriados y gripes en temporadas frías?
- 23 diciembre, 2023
Congestión nasal, dolor de cabeza, estornudos, fiebre baja, escalofríos… son algunos de los síntomas más comunes del resfriado y la gripe y, aunque todos hemos pasado alguna vez por este malestar, no todo el mundo presenta la misma inmunidad o defensas.

- Dennis Sullivan, ganador del premio Abel 2022
- 11 abril, 2022
El profesor Sullivan “es de los pocos matemáticos que, dentro de su mente, es capaz de ver mundos que son solo series de símbolos. Tiene una imagen mental de objetos mucho más abstractos que los objetos geométricos más cotidianos”.

- Entre la Historia y la Matemática
- 30 marzo, 2024
El tránsito hacia una matemática filosófica exige iniciar una quinta revolución matemática; para ello, el estudio de la historia desde el hacer de un matemático es fundamental.

- La formación de un matemático
- 05 julio, 2025
Un matemático es un científico básico, su formación requiere muchos años de preparación académica.
Opinión
Editorial
Los datos personales y el “espionaje de Estado”
El segundo tema se refiere a la veloz aprobación de 16 leyes realizada a principios del presente mes en el Congreso de la Unión.
Las más leídas
Protestan locutores y artistas del doblaje contra la IA
Pese a adeudos con el SAT, gobierno de la CDMX da contrato millonario a Salinas Pliego
Pemex oculta hallazgos de cinco auditorías sobre anomalías internas
Atlixco: la capital de las flores sin protección ante las lluvias
¡Sí o sí! CURP Biométrica será obligatoria a partir de 2026, pese a riesgo de hackers
El estadio “Nido del Halcón” legado de corrupción en Veracruz











Escrito por Daniel Lara
Licenciado en Física por la UNAM y Maestro en Administración de Negocios. Docente de Física y Matemáticas en la UDEG y en la UPA. Actualmente se desempeña en la Dirección General de Estadísticas Económicas del Inegi.