La forma en que pensamos y sentimos está determinada por la interacción entre el cuerpo y el cerebro.

Continuando con la discusión acerca del movimiento y la continuidad, reproduciré algunos pasajes escritos por el filósofo y científico Aristóteles en su obra Física, libro VI. En el apartado El continuo como lo infinitamente divisible, el gran pensador griego demuestra que el continuo no puede estar hecho de un conjunto de indivisibles (átomos) o de puntos (“aquello indivisible en partes”), como lo habían planteado Leucipo, Demócrito y Euclides. Esta definición nos lleva a una contradicción, advirtió Aristóteles, porque “ni los extremos de los puntos pueden ser uno, ya que en un indivisible no puede haber un extremo que sea distinto de otra parte, ni tampoco pueden estar juntos, pues lo que no tiene partes no puede tener extremos, ya que un extremo es distinto de aquel de lo cual es extremo”.
Con este argumento lógico, no solamente demostró Aristóteles la divisibilidad infinita de lo continuo, sino también la del tiempo y del movimiento, como lo prueba su siguiente razonamiento: “si todo movimiento es divisible y si una cosa en movimiento con una velocidad igual recorre una distancia menor en un tiempo menor, entonces el tiempo también será divisible”. Usando este resultado demostró que si “dos cuerpos están en movimiento, el más rápido recorrerá una distancia mayor en un tiempo igual, una distancia igual en un tiempo menor y una distancia mayor en un tiempo menor”, con lo que siempre es posible que el móvil más rápido no solo alcance al móvil más lento, sino que lo rebase, tanto como se quiera. En el caso de Aquiles y la tortuga, por ejemplo, el más veloz entre los aqueos logrará rebasar sin mucha dificultad al reptil más lento del planeta, que se desplaza a una velocidad promedio de 0.040 km/h. Con esta argumentación, el estagirita demostró a Zenón de Elea el error de su lógica.
Sin embargo, para cerrar la discusión planteada por Zenón en sus paradojas, Aristóteles tuvo que demostrar la continuidad del tiempo. Al respecto argumentó: “puesto que todo movimiento es en el tiempo y en todo tiempo algo puede moverse más rápidamente o más lentamente, en todo tiempo podrá haber un movimiento más rápido o más lento”. Si esto es así, razonó, es necesario que el tiempo sea continuo, entendiendo al continuo como aquello “divisible en divisibles siempre divisibles”. Dos mil cien años después, el matemático alemán Georg Cantor le daría la razón al demostrar la densidad del conjunto de los números racionales e irracionales, es decir, la existencia infinita de números racionales e irracionales, entre dos cualesquiera de ellos, respectivamente. Con esta aportación matemática quedó demostrada formalmente la continuidad de la recta real, aunque Aristóteles ya lo había resuelto lógicamente.
Sin embargo, quedaba pendiente un problema todavía por resolver: el carácter infinito del tiempo y magnitud, tanto si son considerados infinitamente pequeños (división infinita) o infinitamente grandes (adición infinita). Ambas respuestas las proporcionó Aristóteles con sus dos tipos de infinito: el infinito potencial, definido como proceso de crecimiento o de división sin final e infinito actual, considerado como “una totalidad completa”. Una vez respondida la pregunta, Aristóteles pasa a las siguientes consideraciones: “si el tiempo es infinito con respecto a sus extremos, así también lo será la longitud”; “si el tiempo es infinito con respecto a la división, así también lo será la longitud”; y “si el tiempo es infinito en ambos respectos, la magnitud será también infinita en ambos respectos”. Guiándose con esta aseveración, Aristóteles demostró lógicamente que es posible recorrer un espacio infinito, pero solo en un tiempo infinito: “no es posible durante un tiempo finito tocar cosas que sean infinitas por su cantidad, pero se las puede tocar si son infinitas por su división, porque en este sentido el tiempo mismo es infinito. Así el tiempo en el que es recorrida una magnitud no es finito sino infinito y las infinitas cosas no son tocadas en un tiempo finito sino en infinitos intervalos de tiempo”. Con esto, Aristóteles zanjó, de una vez y por todas, las paradojas planteadas por Zenón.
No por nada Aristóteles se había ganado el respeto y admiración de Carlos Marx al considerarle como el “pensador dotado de una ciencia verdaderamente enciclopédica”. Aquí vemos, una vez más, la aportación de este gran pensador al mundo del cálculo infinitesimal.
Notas relacionadas


Cuando se aborda el tema de la Inteligencia artificial (IA), a diferencia de algunas décadas atrás en el tiempo, ya no se aborda como ciencia-ficción; ahora la IA es una realidad.

La empresa mexicana ThumbSat diseñó y construyó los satélites en tamaño reducido (de 100 gramos cada uno aproximadamente).

La compañía tecnológica informó a medios especializados que los datos comprometidos incluyen información general, como nombres de usuarios y empresas, pero no contraseñas.
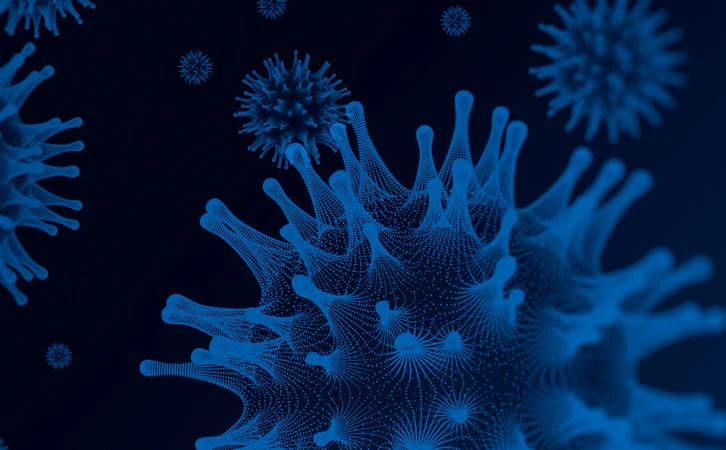
Los resultados mostraron un incremento de 38.3 a 42.6 por ciento los pacientes con afecciones intestinales y cerebrales en 2017 y 2023 respectivamente.
En su Segunda Carta de Relación dice que “la dicha provincia es redonda y está toda cercada de muy altas y ásperas sierras, y lo llano de ella tendrá en torno hasta setenta leguas”.

El vicepresidente brasileño, Geraldo Alckmin, visitará México a finales de agosto, acompañado por ministros y empresarios.

El estudio muestra que las diferencias en la superficie de la Luna están relacionadas con su interior y ha creado el mapa más preciso de su gravedad hasta ahora.

A lo largo de la historia, las dos guerras mundiales han dado lugar a los mayores ecocidios.

El estudio sugiere que los avances científicos están diseñados para monitorear a personas, lo que podría beneficiar a la industria de la vigilancia.

Enjambres de terremotos se incrementan a finales del verano, tras la filtración del agua de deshielo, y disminuyen en primavera.

El mini robot imita con precisión la anatomía de un insecto real.

El desarrollo de la sociedad ha engendrado diversas clases sociales.

Los investigadores calificaron este caso como “una de las mayores filtraciones de datos de la historia”.

Genera hasta 50 escenarios posibles con una antelación de hasta 15 días.
Opinión
Editorial
El optimismo del primer informe presidencial
Como era de esperarse, el primer informe de gobierno de la presidenta Claudia Sheinbaum y séptimo del gobierno de la “Cuarta Transformación” (4T) mostró como principal característica grandes avances en los más importantes aspectos de la vida económica y social de los mexicanos.
Las más leídas
Alistan jornada nacional frente abuso sexual y maltrato infantil
Élite europea trama Revolución de Colores en Serbia, Hungría y Eslovaquia
Primer informe presidencial: un México sin problemas
Jornaleras, abandonadas por el gobierno de Claudia Sheinbaum
El momento histórico en que los rarámuris dominaron el centro y suroeste de Chihuahua











Escrito por Romeo Pérez
Doctor en Física y Matemáticas por la Facultad de Mecánica y Matemáticas de la Universidad Estatal de Lomonosov, de Moscú, Rusia.