Dos herramientas matemáticas de demostración fueron constantes en las obras de Arquímedes: el método exhaustivo, establecido por Eudoxo de Cnido, y el método por reducción al absurdo, formalizado por él mismo. Ambos métodos fueron usados por él; en primer lugar, para calcular áreas del círculo de radio uno, del segmento parabólico y de la espiral que lleva su nombre y, en segundo lugar, para encontrar volúmenes de segmentos de “conoide rectángulo” (paraboloide de revolución), de “conoide obtusángulo” (hiperboloide de revolución) y de esferoide (elipsoide de revolución).
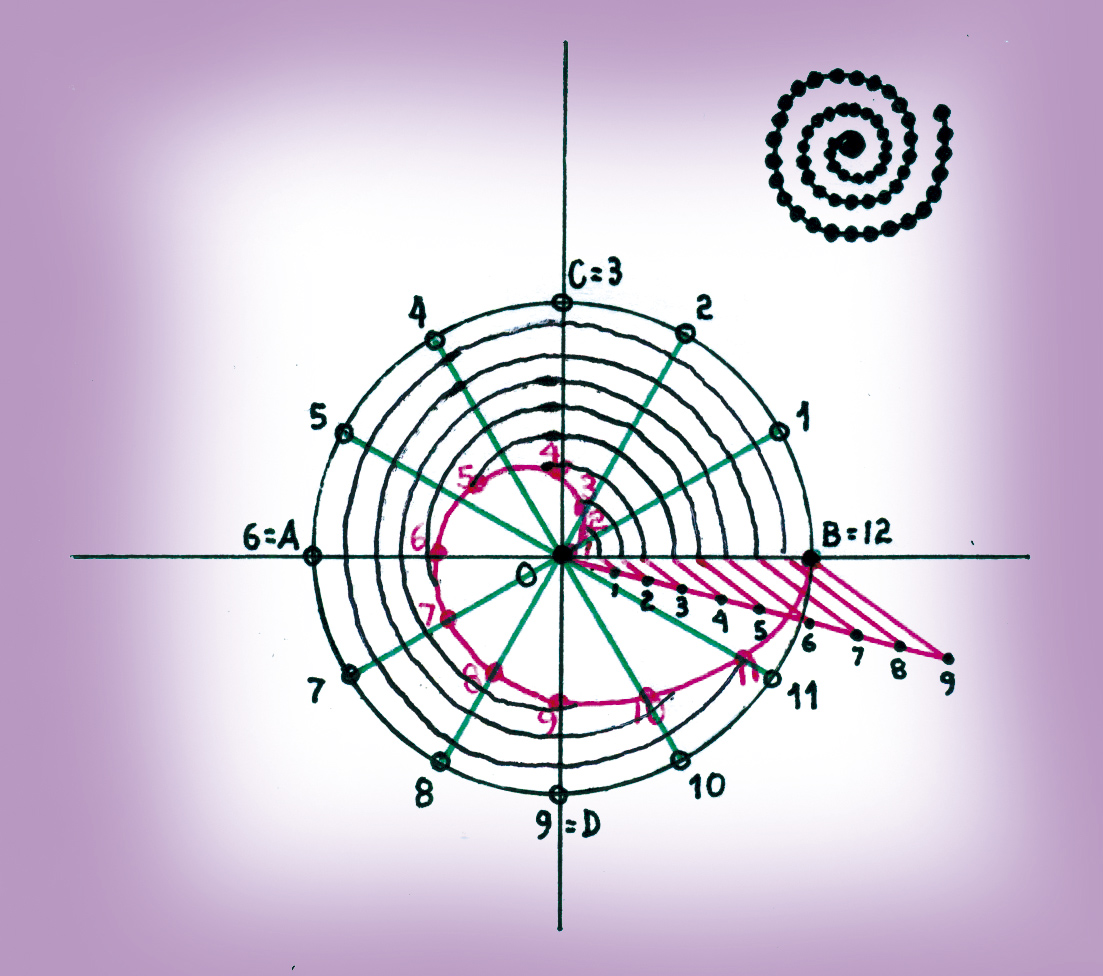
Thomas Little Heath, en su libro The works of Archimedes (págs. 99-188), recoge los trabajos Sobre los conoides y esferoides y Sobre las espirales del sabio de Siracusa. De estas dos obras, me interesa particularmente destacar el trabajo Sobre las espirales, porque, en esta aportación matemática, se vislumbra ya la síntesis del cálculo integral y diferencial. Arquímedes comienza construyendo su espiral partiendo de un punto que se mueve sobre una recta a una velocidad uniforme, recta que gira sobre un punto fijo (origen) con una velocidad angular uniforme.
Para continuar con su investigación, el genio de Siracusa demuestra que el área de dicha espiral, en su primera vuelta, cubre la tercera parte del círculo que la envuelve. La solución a esta afirmación trajo consigo la respuesta a uno de los tres problemas clásicos de la Grecia antigua, el problema de la trisección del ángulo que, con la cuadratura del círculo y la duplicación del cubo, habían resistido los embates de los más eminentes matemáticos griegos.
La espiral de Arquímedes, que “evoca el infinito” y “triseca” ángulos, concentra el cálculo infinitesimal muy desarrollado para su tiempo. Un ejemplo de esta concentración se encuentra en la siguiente proposición: “el área acotada por la primera vuelta de la espiral y la línea inicial es igual a la tercera parte del primer círculo (que la envuelve)” (Proposición 24, pág. 178).
Hoy la ecuación de dicha espiral se puede expresar en coordenadas polares de la forma r (θ)=aθ, donde r es la distancia al origen, a es una constante y θ es el ángulo girado. Se requiere encontrar el área de la espiral cuando el ángulo polar varía de 0 a 2π en relación con el área del círculo circunscrito de radio 2πa. Es inmediato calcular el área de este círculo por medio de la fórmula πr2 = π (2π a)2 y de la espiral, por medio de la integral en coordenadas polares, tomando como integrando la función polar r2/2 en el intervalo [0, 2π]. Usando algunas operaciones básicas de la integral, obtenemos en seguida que π (2π a)2/3, corresponde al área de la espiral, la cual es la tercera parte del primer círculo que la circunscribe. Esta maquinaria matemática, sin embargo, no existía en aquellos tiempos, por eso Arquímedes procede de la siguiente manera: divide el círculo de radio 2π a en sectores de amplitud θ=2π /n; con n en los números naturales. Luego, en cada sector circular, examina el arco de la espiral que queda dentro del mismo sector y acota el área correspondiente a dicho arco de la espiral entre las áreas de dos sectores circulares. Posteriormente calcula el área del sector circular más grande inscrito en cada arco de la espiral y el área del sector circular más pequeño circunscrito a cada arco de la espiral, y por medio del método exhaustivo va cubriendo progresivamente la espiral con cada sector circular inscrito y circunscrito tantas veces como se quiera. Después, suma el área de todos lo sectores circulares más grandes inscritos en cada arco de la espiral y el área de todos los sectores circulares más pequeños circunscritos a cada arco. Finalmente, Arquímedes aplica dos veces el método por reducción al absurdo para comprobar la veracidad de la Proposición 24 de su libro Sobre las espirales.
Con esta aportación, Arquímedes se había adelantado a los matemáticos de mediados y último tercio del Siglo XVII como Cavalieri, Pascal, Newton y Bernoulli, quienes usaron formalmente las coordenadas polares para resolver problemas relativos a áreas, longitud de arcos parabólicos y tangentes respectivamente.
Notas relacionadas

- Avanzan estudios para prótesis visuales
- 07 agosto, 2019
La intención es lograr un lente de material blando que logre un acercamiento, en un primer prototipo, de 32 por ciento con respecto a la visualización normal.

- Las tierras raras de Groenlandia
- 15 febrero, 2025
Groenlandia es un país autónomo que, paradójicamente, pertenece al reino de Dinamarca y controla su política exterior y monetaria.

- Niels Steensen, el padre de la geología moderna
- 24 octubre, 2021
Antes se creía que el parecido entre los fósiles y los seres vivos era gracias a un espíritu animador o vegetativo. Fue gracias al médico Niels Steensen que se reconoció la pertenencia de fósiles a seres vivos.

- Los bosques también se enferman
- 08 enero, 2023
No es raro encontrar bosques enfermos: aquéllos con hojas amarillas o cafés, troncos llenos de grumos resinosos, follaje manchado y, en los casos más graves, la presencia masiva de plantas o insectos parásitos.

- Gaspard Monge: un conde considerado padre de la geometría diferencial
- 12 diciembre, 2021
Fue uno de los matemáticos políticos que apoyó decididamente la Revolución Francesa. En 1794 formó parte del comité de organización de la Ecole Centrale oles Travaux Rublics (Escuela Politécnica de París) donde escribió una de sus obras más famosas: Aplic

- Nuevas instalaciones de Tesla podrían llegar a México
- 10 febrero, 2023
La empresa Tesla, del multimillonario Elon Musk, pretende fabricar nuevas instalaciones en tres estados de la República Mexicana.

- Meteoritos, partículas y colisiones
- 24 mayo, 2020
Que la energía cinética (antes llamada fuerza viva) representa el cambio del movimiento mecánico en otra forma de movimiento.

- ¿Por qué aumentan los resfriados y gripes en temporadas frías?
- 23 diciembre, 2023
Congestión nasal, dolor de cabeza, estornudos, fiebre baja, escalofríos… son algunos de los síntomas más comunes del resfriado y la gripe y, aunque todos hemos pasado alguna vez por este malestar, no todo el mundo presenta la misma inmunidad o defensas.

- Cálculo infinitesimal en la espiral de Arquímedes
- 05 enero, 2021
Arquímedes se había adelantado a los matemáticos de mediados y último tercio del Siglo XVII como Cavalieri, Pascal, Newton y Bernoulli.

- La edición genética por CRISPR/Cas9
- 28 junio, 2020
El sistema CRISPR/Cas9 es considerado como el método más simple, versátil y preciso de manipulación genética.
- Vacunación infantil y austeridad en México
- 26 febrero, 2023
Las consecuencias de la desatención del programa de vacunación infantil ya se están manifestando, pues hay rebrotes de Sarampión y Tuberculosis.

- NASA revela nuevas fotos del Telescopio Webb
- 12 julio, 2022
Ayer, el Telescopio Espacial James Webb reveló la imagen más clara hasta la fecha del universo primitivo, que se remonta a 13 mil millones de años, dijo la NASA el lunes.

- Construirán en Chile el telescopio óptico más grande del mundo
- 30 agosto, 2024
Tiene como objetivo ampliar la compresión del universo y contará con uno de los espejos más avanzados jamás creados.

- El capitalismo y su incompatibilidad con la Ecología
- 18 noviembre, 2023
Aquí una síntesis de una cercana catástrofe ambiental y la urgencia de replantear nuestro enfoque económico para garantizar la supervivencia a largo plazo de la vida como la conocemos en nuestro planeta.

- ¿Es la matemática una ciencia?
- 18 junio, 2023
Alguna vez escuché decir que la matemática no es una ciencia al no someterse al método científico, pero en ciertos trabajos se ha exigido a los estudiantes utilizar el método científico, ¿cómo es posible? Aquí explico.
Opinión
Editorial
La reforma salarial y los intereses patronales
Más de ocho meses han transcurrido después de que el Senado de la República aprobara una reforma que modifica el Artículo 123º Constitucional con el fin de mejorar las condiciones de vida de los trabajadores y sus familias.











Escrito por Romeo Pérez
Doctor en Física y Matemáticas por la Facultad de Mecánica y Matemáticas de la Universidad Estatal de Lomonosov, de Moscú, Rusia.