Dos herramientas matemáticas de demostración fueron constantes en las obras de Arquímedes: el método exhaustivo, establecido por Eudoxo de Cnido, y el método por reducción al absurdo, formalizado por él mismo. Ambos métodos fueron usados por él; en primer lugar, para calcular áreas del círculo de radio uno, del segmento parabólico y de la espiral que lleva su nombre y, en segundo lugar, para encontrar volúmenes de segmentos de “conoide rectángulo” (paraboloide de revolución), de “conoide obtusángulo” (hiperboloide de revolución) y de esferoide (elipsoide de revolución).
Thomas Little Heath, en su libro The works of Archimedes (págs. 99-188), recoge los trabajos Sobre los conoides y esferoides y Sobre las espirales del sabio de Siracusa. De estas dos obras, me interesa particularmente destacar el trabajo Sobre las espirales, porque, en esta aportación matemática, se vislumbra ya la síntesis del cálculo integral y diferencial. Arquímedes comienza construyendo su espiral partiendo de un punto que se mueve sobre una recta a una velocidad uniforme, recta que gira sobre un punto fijo (origen) con una velocidad angular uniforme.
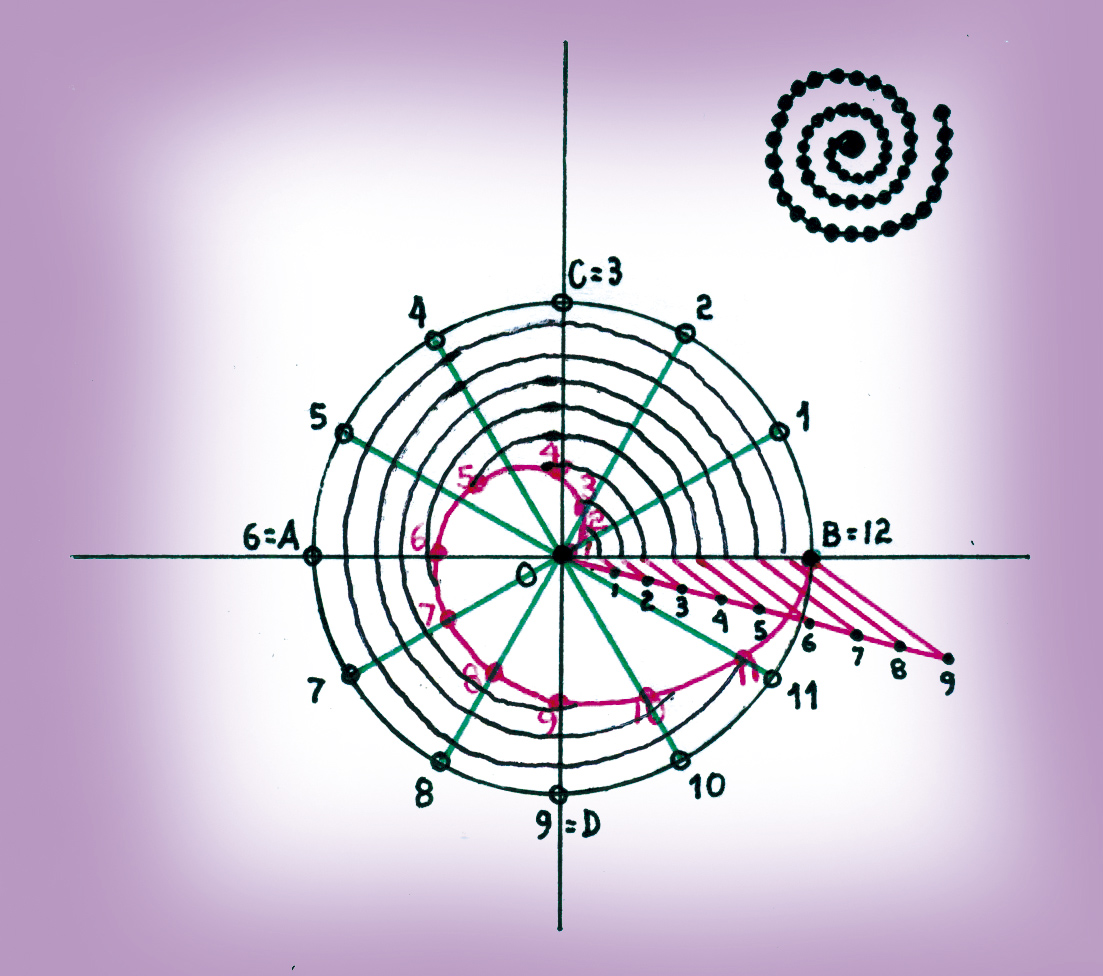
Para continuar con su investigación, el genio de Siracusa demuestra que el área de dicha espiral, en su primera vuelta, cubre la tercera parte del círculo que la envuelve. La solución a esta afirmación trajo consigo la respuesta a uno de los tres problemas clásicos de la Grecia antigua, el problema de la trisección del ángulo que, con la cuadratura del círculo y la duplicación del cubo, habían resistido los embates de los más eminentes matemáticos griegos.
La espiral de Arquímedes, que “evoca el infinito” y “triseca” ángulos, concentra el cálculo infinitesimal muy desarrollado para su tiempo. Un ejemplo de esta concentración se encuentra en la siguiente proposición: “el área acotada por la primera vuelta de la espiral y la línea inicial es igual a la tercera parte del primer círculo (que la envuelve)” (Proposición 24, pág. 178).
Hoy la ecuación de dicha espiral se puede expresar en coordenadas polares de la forma r (θ)=aθ, donde r es la distancia al origen, a es una constante y θ es el ángulo girado. Se requiere encontrar el área de la espiral cuando el ángulo polar varía de 0 a 2π en relación con el área del círculo circunscrito de radio 2πa. Es inmediato calcular el área de este círculo por medio de la fórmula πr2 = π (2π a)2 y de la espiral, por medio de la integral en coordenadas polares, tomando como integrando la función polar r2/2 en el intervalo [0, 2π]. Usando algunas operaciones básicas de la integral, obtenemos en seguida que π (2π a)2/3, corresponde al área de la espiral, la cual es la tercera parte del primer círculo que la circunscribe. Esta maquinaria matemática, sin embargo, no existía en aquellos tiempos, por eso Arquímedes procede de la siguiente manera: divide el círculo de radio 2π a en sectores de amplitud θ=2π /n; con n en los números naturales. Luego, en cada sector circular, examina el arco de la espiral que queda dentro del mismo sector y acota el área correspondiente a dicho arco de la espiral entre las áreas de dos sectores circulares. Posteriormente calcula el área del sector circular más grande inscrito en cada arco de la espiral y el área del sector circular más pequeño circunscrito a cada arco de la espiral, y por medio del método exhaustivo va cubriendo progresivamente la espiral con cada sector circular inscrito y circunscrito tantas veces como se quiera. Después, suma el área de todos lo sectores circulares más grandes inscritos en cada arco de la espiral y el área de todos los sectores circulares más pequeños circunscritos a cada arco. Finalmente, Arquímedes aplica dos veces el método por reducción al absurdo para comprobar la veracidad de la Proposición 24 de su libro Sobre las espirales.
Con esta aportación, Arquímedes se había adelantado a los matemáticos de mediados y último tercio del Siglo XVII como Cavalieri, Pascal, Newton y Bernoulli, quienes usaron formalmente las coordenadas polares para resolver problemas relativos a áreas, longitud de arcos parabólicos y tangentes respectivamente.
Notas relacionadas

- Se pierde la batalla contra el calentamiento global
- 18 junio, 2019
En los últimos 400 mil años, la concentración de CO2 atmosférico varió de 180 a 300 ppm

- Epigenética, crecimiento y salud animal (I de II)
- 05 julio, 2021
En febrero de 2001 se publicaron los resultados de casi una década de trabajo del prometedor programa de investigación genética: Proyecto Genoma Humano, el cual logró descifrar el 90 por ciento del genoma humano.

- William Hamilton: el mejor matemático de Irlanda
- 17 octubre, 2021
Los problemas personales no afectaron su brillante carrera académica; su jornada incluía largas horas de concentración.

Enjambres de terremotos se incrementan a finales del verano, tras la filtración del agua de deshielo, y disminuyen en primavera.

- Desafíos ambientales: la deforestación en México
- 30 marzo, 2024
A pesar del indiscutible rol que juegan los bosques, cada año disminuye su superficie debido al cambio de uso de suelo, tala clandestina e incendios forestales. De 2000 a 2018 se perdieron 13 mil 777 hectáreas.

- ¿Por qué dependemos de los bosques?
- 12 junio, 2022
Los daños causados al planeta comienzan a pasarnos factura. Las tasas de deforestación han afectado gravemente las distintas funciones de los bosques, además, su papel como regulador del clima está siendo severamente afectado.

El eclipse solar total será el próximo 8 de abril.

- El modelamiento matemático
- 27 marzo, 2023
El matemático que opera y crea los objetos que la matemática estudia, si puede tener compromiso con la realidad, éste lo conduce a un proceso de establecer isovalencias entre los problemas reales y los objetos matemáticos.
- Entre la filosofía y la Matemática
- 24 marzo, 2024
Mientras el trabajo matemático tiene reglas, axiomas, y su libertad está en función de estar gobernado por sistemas formales; en el trabajo filosófico...

- CDMX, la más conectada… y la más desigual
- 11 noviembre, 2021
Este miércoles, la Ciudad de México fue reconocida como la ciudad con más puntos conectados a internet en el mundo, superando incluso a Moscú, Rusia. En contraste, también ostenta el primer lugar en mayor desigualdad.

- Una batalla ganada contra el SARS-COV2
- 30 enero, 2022
Actualmente, diferentes grupos de científicos alrededor del mundo trabajan en la búsqueda y el desarrollo de tratamientos para combatir el Covid-19; el reto es que éstos sean eficaces contra las variantes actuales y futuras.

El hallazgo sucedió en mayo de 2022 por el paleontólogo Damien Boschetto, quien observó en el borde de un acantilado derrumbado un hueso expuesto.

Carl Jacobi desarrolló una intensa labor de investigación, su obra científica publicada por la Academia de Ciencias de Berlín asciende a ocho volúmenes.

Investigadores del Instituto Tecnológico de Massachusetts demostraron la existencia de una "red lingüística universal" en hablantes de 45 lenguas, un hallazgo que podría revelar los procesos cognitivos base de todo el lenguaje hablado.
Los nuevos ambientes activan en nuestro organismo la producción de dopamina, sustancia que promueve el aprendizaje asociativo.
Opinión
Editorial
La reforma salarial y los intereses patronales
Más de ocho meses han transcurrido después de que el Senado de la República aprobara una reforma que modifica el Artículo 123º Constitucional con el fin de mejorar las condiciones de vida de los trabajadores y sus familias.











Escrito por Romeo Pérez
Doctor en Física y Matemáticas por la Facultad de Mecánica y Matemáticas de la Universidad Estatal de Lomonosov, de Moscú, Rusia.